Ideenbewertung mit der Paarvergleichsmatrix

Paarvergleiche in der Ideenbewertung

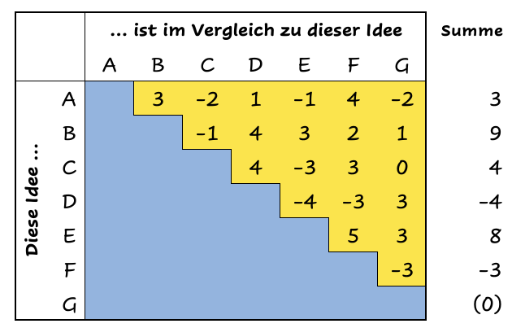
Es gibt gute Gründe, die Ideenbewertung mit Paarvergleichen statt mit der Punktevergabe durchzuführen. Die Paarvergleichsmatrix ist eine Methode, die Paarvergleiche nutzt, um ein Ranking unter mehreren Ideen zu ermitteln. Die Methode ist sehr einfach in der Durchführung, wird aber für eine große Anzahl von Ideen schnell aufwendig. Die Anzahl der notwendigen Vergleiche wächst nämlich quadratisch mit der Anzahl der Ideen. Werden für die Bewertung von sieben Ideen 21 Paarvergleiche benötigt (siehe Titelgrafik), braucht es für 14 Ideen (die doppelte Zahl) schon 91 Vergleiche (mehr als das Vierfache).

Diese Paarvergleichsmatrix darf nicht mit der gleichnamigen Matrix verwechselt werden, die im Analytic Hierarchy Process verwendet wird.

Anwendung der Paarvergleichsmatrix

Die Ideen bilden die Spalten- und Reihenüberschriften der Matrix. Die Ideen werden paarweise betrachtet: Jede Idee wird mit jeder anderen verglichen. Die Teilnehmer können jeden Paarvergleich mit -1, 0 oder 1 bewerten:

• 1: Die erste Idee ist besser als die zweite.
• 0: Die Ideen sind gleichwertig.
• -1: Die erste Idee ist schlechter als die zweite.

Die Zahlen alle Teilnehmer werden dann zusammengerechnet und an der entsprechenden Stelle im oberen Dreiecksteil der Tabelle (gelb) eingetragen. Zum Schluss bildet man die Reihensummen. Das Ergebnis stellt den Wert der jeweiligen Idee relativ zu den anderen dar.

Beispiel

Fünf Workshop-Teilnehmer bewerten die sieben Ideen A bis G. Die Tabelle in der Titelgrafik zeigt die entsprechende Paarvergleichsmatrix. Die Experten sind sich einig, dass Idee E besser ist, als Idee F. An allen anderen Stellen könnten sie sich einig gewesen sein, aber das ist aus den Summen nicht abzulesen. Die Summe 1 beispielsweise könnte aus den Bewertungen (-1, -1, 1, 1, 1) entstanden sein, was die größtmögliche Uneinigkeit repräsentiert.

In der Zeile G müssen keine Paarvergleiche durchgeführt werden, weil die Ergebnisse in den Zeilen A bis F alle schon bestimmt sind. Demzufolge hat Idee G die Bewertung 0, und alle anderen Bewertungen sind relativ zu diesem Wert. Das Ranking, das sich aus diesen Bewertungen ergibt, lautet:

1. Idee B
2. Idee E
3. Idee C
4. Idee A
5. Idee G
6. Idee F
7. Idee D

Problem: Fehlende Transitivität

Ein Teilnehmer könnte die folgenden drei Bewertungen eingeben:

• G ist besser als E.
• E ist besser als F.
• F ist besser als G.

Diese drei Bewertungen machen zusammen wenig Sinn, weil die Reihenfolge der Ideen nicht feststellbar ist: Die „besser als“-Relation bildet eine Schleife. Obwohl es wenig Sinn macht, lässt das Verfahren solche Kombinationen zu. Eigentlich sollte man erwarten, dass aus G ist besser als E und E ist besser als F folgen muss: G ist besser als F. Diese Eigenschaft wird Transitivität genannt. Die Theoretiker streiten sich darüber, ob solche Konfigurationen zulässig sein sollen oder nicht.

Links

Kompaktwissen Ideenbewertung