Gruppenideenbewertung: Median or Mean?

Ideenbewertung in der Gruppe

Ideen werden fast immer von Gruppen bewertet. Entweder am Ende eines Innovationsworkshops oder in einem dedizierten Bewertungsworkshop sitzen Experten zusammen, um gemeinsam aus einer Menge von Ideen die besten zu identifizieren.

Entgegen der Erwartung vieler Kunden ist die Bewertung von Ideen viel schwieriger als das Generieren. Viele der Schwierigkeiten der Ideenbewertung entstehen, weil eine Gruppe beteiligt ist.

Es ist fast unvermeidlich, dass es in einer Gruppe zu abweichenden Urteilen der Gruppenmitglieder kommt. Eine Ursache dafür sind die versteckten Profile – unterschiedliche Vorstellungen von der selben Sache. Der Moderator oder Innovationsmanager hat dann das Problem, dass er die verschiedenen Urteile zusammenführen muss, um zu einem Gesamturteil zu kommen. selbst bei dieser scheinbar sehr einfachen Aufgabe kann man schwerwiegende Fehler machen, zum Beispiel indem man die Urteile in der falschen Reihenfolge aggregiert.

In diesem Artikel beschreiben wir einen subtilen Fehler der Gruppenideenbewertung, der sehr häufig begangen wird. Das Argument ist zwar theoretisch, hat aber unmittelbare praktische Konsequenzen. Die Erkenntnis ist im Rahmen unserer Idea Engineering-Forschung mit der Universität Magdeburg zusammen entstanden.

Aggregation von Urteilen bei der Gruppenideenbewertung

Fast immer wird für die Bewertung von Ideen eine Art von Punktevergabe verwendet. Im Innovationsmanagement wird beispielsweise die Nutzwertanalyse gerne eingesetzt, bei der den Ideen Punkte auf einer Skala von 1 bis 5 oder 1 bis 10 gegeben werden.

In einer Gruppe hat der Moderator zwei Möglichkeiten: entweder die Gruppe einigt sich auf die Punkte, die vergeben werden, oder die Mitglieder vergeben ihre Punkte alleine, und sie werden dann hinterher rechnerisch zusammengeführt. Findet die Bewertung räumlich oder zeitlich getrennt statt, bleibt nur die zweite Option.

Mittelwert und Median

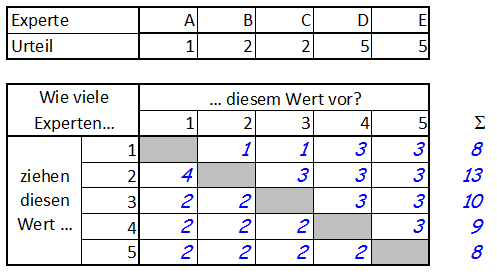
Um verschiedene Punktzahlen zu einem Gesamturteil zusammenzuführen greifen die meisten Menschen zum (arithmetischen) Mittelwert (engl.: Mean). In der Titelgrafik zeigen wir ein Beispiel mit den fünf Experten A, B, C, D und E, die eine Idee mit 1, 1, 2, 5 bzw. 5 Punkten bewertet haben. Das arithmetische Mittel dieser fünf Bewertungen ist (1+2+2+5+5)/5 = 3.

Eine Alternative zum Mittelwert ist der Median. Der Median einer Menge von Zahlen ist definiert als diejenige, die in der Mitte steht, wenn alle Zahlen der Größe nach aufgereiht werden. Der Median der fünf Expertenbewertungen 1, 2, 2, 5, 5 in der Titelgrafik ist demzufolge die 2.

Das Argument für den Median

Wie zeigen nun ein theoretisches Argument, das gegen die Verwendung des arithmetischen Mittelwertes und für den Median spricht.

Ein Ziel der Gruppenideenbewertung ist, unter den Teilnehmern Konsens über das Endergebnis zu erzielen. Wir können den Konsens prüfen, indem wir in einem Gedankenexperiment eine Wahl durchführen, bei der jedes Einzelurteil jedem anderen Einzelurteil gegenübergestellt wird und die Experten darüber abstimmen, welchem Einzelurteil sie den Vorzug geben. Das Einzelurteil, das auf diese Weise die meisten Stimmen erhält, ist dann das aggregierte Gruppenergebnis.

Man kann relativ leicht mathematisch beweisen, dass der Median von allen Einzelurteilen dasjenige ist, das diese Wahl immer gewinnt. Es gibt zwar Fälle, in denen das arithmetische Mittel mit dem Median übereinstimmt und damit auch zum Mehrheitsergebnis führt, aber im allgemeinen werden die beiden Mittelwerte unterschiedlich sein.

Beispiel

Die Titelgrafik zeigt das bereits beschriebene Beispiel mit den fünf Bewertungen 1, 2, 2, 5 und 5, mit arithmetischem Mittel 3 und Median 2.

Die Tabelle zeigt die Stimmen für jeden paarweisen Vergleich. Wir lesen zum Beispiel als Antwort auf die Frage Wie viele Experten ziehen den Wert 2 dem Wert 1 vor? die Zahl 4. Das Ergebnis kommt wie folgt zustande:

• Experte A, der mit 1 bewertet hat, zieht den Wert 2 dem Wert 1 nicht vor.
• Experte B, der mit 2 bewertet hat, zieht den Wert 2 dem Wert 1 vor.
• Experte C, der mit 2 bewertet hat, zieht den Wert 2 dem Wert 1 vor.
• Experte D, der mit 5 bewertet hat, zieht den Wert 2 dem Wert 1 vor.
• Experte E, der mit 5 bewertet hat, zieht den Wert 2 dem Wert 1 vor.

Bildet man die Zeilensummen der Tabelle, erkennt man, dass der Median 2 mit 13 die meisten Stimmen erhält. Das arithmetische Mittel 3 dagegen bekommt nur 10 Stimmen. Etwas einfacher kommt man zum gleichen Ergebnis, wenn man erkennt, dass die drei Experten mit den Bewertungen 1, 2 und 2 der Bewertung 2 den Vorzug vor der Bewertung 3 geben, auf der anderen Seite aber nur die beiden Experten mit der Bewertung 5 die 3 der 2 vorziehen.

Kommentar

Den Median zur Aggregation von Meinungen in der Gruppenideenbewertung zu verwenden ist ungewöhnlich, weil wir in so vielen ähnlichen Situationen im Leben dem arithmetischen Mittel begegnen, zum Beispiel bei der Bildung der Abiturnote aus den einzelnen Fachnoten. Wenn man im Beispiel die Werte (1, 2, 2, 5, 5) betrachtet, fühlt sich der Wert (1+2+2+5+5)/5=3 „irgendwie richtiger an“ als die 1 2 2 5 5. Nichtsdestotrotz würde die 3 in einer Abstimmung gegen die 2 unterliegen.

 

Zuletzt aktualisiert am 28. Juni 2015 von Graham Horton